Difference between revisions of "User:Jhurley/sandbox"

From Enviro Wiki
Jump to: navigation, search
(→‎Modeling Diffusion)
(→‎Analysis of PFAS Concentrations in Soil and Porewater)
 
Line 1: Line 1:
−
Groundwater migrates from areas of higher [[wikipedia: Hydraulic head | hydraulic head]] toward lower hydraulic head, transporting dissolved solutes through the combined processes of [[wikipedia: Advection | advection]] and [[wikipedia: Dispersion | dispersion]]. Advection refers to the bulk movement of solutes carried by flowing groundwater. Dispersion refers to the spreading of the contaminant plume from highly concentrated areas to less concentrated areas. In many groundwater transport models, solute transport is described by the advection-dispersion-reaction equation in which dispersion coefficients can be calculated as the sum of molecular diffusion, mechanical dispersion, and macrodispersion.
+
==Lysimeters for Measuring PFAS Concentrations in the Vadose Zone==
−
 
+
[[Perfluoroalkyl and Polyfluoroalkyl Substances (PFAS) | PFAS]] are frequently introduced to the environment through soil surface applications which then transport through the vadose zone to reach underlying groundwater receptors. Due to their unique properties and resulting transport and retention behaviors, PFAS in the vadose zone can be a persistent contaminant source to underlying groundwater systems. Determining the fraction of PFAS present in the mobile porewater relative to the total concentrations in soils is critical to understanding the risk posed by PFAS in vadose zone source areas. Lysimeters are instruments that have been used by agronomists and vadose zone researchers for decades to determine water flux and solute concentrations in unsaturated porewater. Lysimeters have recently been developed as a critical tool for field investigations and characterizations of PFAS impacted source zones.  
 
<div style="float:right;margin:0 0 2em 2em;">__TOC__</div>
 
<div style="float:right;margin:0 0 2em 2em;">__TOC__</div>
  
 
'''Related Article(s):'''
 
'''Related Article(s):'''
  
−
*[[Dispersion and Diffusion]]
+
*[[Perfluoroalkyl and Polyfluoroalkyl Substances (PFAS)]]
−
*[[Sorption of Organic Contaminants]]
+
*[[PFAS Transport and Fate]]
−
*[[Plume Response Modeling]]
 
−
 
 
−
'''CONTRIBUTOR(S):''' [[Dr. Charles Newell, P.E.|Dr. Charles Newell]] and  [[Dr. Robert Borden, P.E.|Dr. Robert Borden]]
 
−
 
 
−
'''Key Resource(s):'''
 
−
 
 
−
*[http://hydrogeologistswithoutborders.org/wordpress/1979-english/ Groundwater]<ref name="FandC1979">Freeze, A., and Cherry, J., 1979. Groundwater, Prentice-Hall, Englewood Cliffs, New Jersey, 604 pages. Free download from [http://hydrogeologistswithoutborders.org/wordpress/1979-english/ Hydrogeologists Without Borders].</ref>, Freeze and Cherry, 1979.
 
−
*[https://gw-project.org/books/hydrogeologic-properties-of-earth-materials-and-principles-of-groundwater-flow/ Hydrogeologic Properties of Earth Materials and Principals of Groundwater Flow]<ref name="Woessner2020">Woessner, W.W., and Poeter, E.P., 2020. Properties of Earth Materials and Principals of Groundwater Flow, The Groundwater Project, Guelph, Ontario, 207 pages. Free download from [https://gw-project.org/books/hydrogeologic-properties-of-earth-materials-and-principles-of-groundwater-flow/ The Groundwater Project].</ref>, Woessner and Poeter, 2020.
 
−
 
 
−
==Groundwater Flow==
 
−
[[File:Newell-Article 1-Fig1r.JPG|thumbnail|left|400px|Figure 1. Hydraulic gradient (typically described in units of m/m or ft/ft) is the difference in hydraulic head from Point A to Point B (ΔH) divided by the distance between them (ΔL). In unconfined aquifers, the hydraulic gradient can also be described as the slope of the water table (Adapted from course notes developed by Dr. R.J. Mitchell, Western Washington University).]]
 
−
Groundwater flows from areas of higher [[wikipedia: Hydraulic head | hydraulic head]] (a measure of pressure and gravitational energy) toward areas of lower hydraulic head (Figure 1). The rate of change (slope) of the hydraulic head is known as the hydraulic gradient. If groundwater is flowing and contains dissolved contaminants it can transport the contaminants by advection from areas with high hydraulic head toward lower hydraulic head zones, or “downgradient”.
 
−
 
 
−
==Darcy's Law==
 
−
{| class="wikitable" style="float:right; margin-left:10px;text-align:center;"
 
−
|+Table 1.  Representative values of total porosity (''n''), effective porosity (''n<sub>e</sub>''), and hydraulic conductivity (''K'') for different aquifer materials<ref name="D&S1997">Domenico, P.A. and Schwartz, F.W., 1997. Physical and Chemical Hydrogeology, 2nd Ed. John Wiley & Sons, 528 pgs. ISBN 978-0-471-59762-9.  Available from: [https://www.wiley.com/en-us/Physical+and+Chemical+Hydrogeology%2C+2nd+Edition-p-9780471597629 Wiley]</ref><ref>McWhorter, D.B. and Sunada, D.K., 1977. Ground-water hydrology and hydraulics. Water Resources Publications, LLC, Highlands Ranch, Colorado, 304 pgs. ISBN-13: 978-1-887201-61-2 Available from: [https://www.wrpllc.com/books/gwhh.html Water Resources Publications]</ref><ref name="FandC1979" />
 
−
|-
 
−
!Aquifer Material
 
−
!Total Porosity<br /><small>(dimensionless)</small>
 
−
!Effective Porosity<br /><small>(dimensionless)</small>
 
−
!Hydraulic Conductivity<br /><small>(meters/second)</small>
 
−
|-
 
−
| colspan="4" style="text-align: left; background-color:white;" |'''Unconsolidated'''
 
−
|-
 
−
|Gravel||0.25 — 0.44||0.13 — 0.44||3×10<sup>-4</sup> — 3×10<sup>-2</sup>
 
−
|-
 
−
|Coarse Sand||0.31 — 0.46||0.18 — 0.43||9×10<sup>-7</sup> — 6×10<sup>-3</sup>
 
−
|-
 
−
|Medium Sand||—||0.16 — 0.46||9×10<sup>-7</sup> — 5×10<sup>-4</sup>
 
−
|-
 
−
|Fine Sand||0.25 — 0.53||0.01 — 0.46||2×10<sup>-7</sup> — 2×10<sup>-4</sup>
 
−
|-
 
−
|Silt, Loess||0.35 — 0.50||0.01 — 0.39||1×10<sup>-9</sup> — 2×10<sup>-5</sup>
 
−
|-
 
−
|Clay||0.40 — 0.70||0.01 — 0.18||1×10<sup>-11</sup> — 4.7×10<sup>-9</sup>
 
−
|-
 
−
| colspan="4" style="text-align: left; background-color:white;" |'''Sedimentary and Crystalline Rocks'''
 
−
|-
 
−
|Karst and Reef Limestone||0.05 — 0.50||—||1×10<sup>-6</sup> — 2×10<sup>-2</sup>
 
−
|-
 
−
|Limestone, Dolomite||0.00 — 0.20||0.01 — 0.24||1×10<sup>-9</sup> — 6×10<sup>-6</sup>
 
−
|-
 
−
|Sandstone||0.05 — 0.30||0.10 — 0.30||3×10<sup>-10</sup> — 6×10<sup>-6</sup>
 
−
|-
 
−
|Siltstone||—||0.21 — 0.41||1×10<sup>-11</sup> — 1.4×10<sup>-8</sup>
 
−
|-
 
−
|Basalt||0.05 — 0.50||—||2×10<sup>-11</sup> — 2×10<sup>-2</sup>
 
−
|-
 
−
|Fractured Crystalline Rock||0.00 — 0.10||—||8×10<sup>-9</sup> — 3×10<sup>-4</sup>
 
−
|-
 
−
|Weathered Granite||0.34 — 0.57||—||3.3×10<sup>-6</sup> — 5.2×10<sup>-5</sup>
 
−
|-
 
−
|Unfractured Crystalline Rock||0.00 — 0.05||—||3×10<sup>-14</sup> — 2×10<sup>-10</sup>
 
−
|}
 
−
In&nbsp;unconsolidated&nbsp;geologic settings (gravel, sand, silt, and clay) and highly fractured systems, the rate of groundwater movement can be expressed using [[wikipedia: Darcy's law | Darcy’s Law]]. This law is a fundamental mathematical relationship in the groundwater field and can be expressed this way:
 
−
 
 
−
[[File:Newell-Article 1-Equation 1rr.jpg|center|500px]]
 
−
 
 
−
::Where:
 
−
:::''Q'' = Flow rate (Volume of groundwater flow per time, such as m<sup>3</sup>/yr)
 
−
:::''A'' = Cross sectional area perpendicular to groundwater flow (length<sup>2</sup>, such as m<sup>2</sup>)
 
−
:::''V<sub>D</sub>'' = “Darcy Velocity”; describes groundwater flow as the volume of flow through a unit of cross-sectional area (units of length per time, such as ft/yr)
 
−
:::''K'' = Hydraulic Conductivity (sometimes called “permeability”) (length per time)
 
−
:::''ΔH'' = Difference in hydraulic head between two lateral points (length)
 
−
:::''ΔL'' = Distance between two lateral points (length)
 
−
 
 
−
[https://en.wikipedia.org/wiki/Hydraulic_conductivity Hydraulic conductivity] (Table 1 and Figure 2) is a measure of how easily groundwater flows through a porous medium, or alternatively, how much energy it takes to force water through a porous medium. For example, fine sand has smaller pores with more frictional resistance to flow, and therefore lower hydraulic conductivity compared to coarse sand, which has larger pores with less resistance to flow (Figure 2).
 
−
 
 
−
[[File:AdvectionFig2.PNG|400px|thumbnail|left|Figure 2. Hydraulic conductivity of selected rocks<ref>Heath, R.C., 1983. Basic ground-water hydrology, U.S. Geological Survey Water-Supply Paper 2220, 86 pgs. [//www.enviro.wiki/images/c/c4/Heath-1983-Basic_groundwater_hydrology_water_supply_paper.pdf Report pdf]</ref>.]]
 
−
Darcy’s Law was first described by Henry Darcy (1856)<ref>Brown, G.O., 2002. Henry Darcy and the making of a law. Water Resources Research, 38(7), p. 1106. [https://doi.org/10.1029/2001wr000727 DOI: 10.1029/2001WR000727] [//www.enviro.wiki/images/4/40/Darcy2002.pdf Report.pdf]</ref> in a report regarding a water supply system he designed for the city of Dijon, France. Based on his experiments, he concluded that the amount of water flowing through a closed tube of sand (dark grey box in Figure 3) depends on (a) the change in the hydraulic head between the inlet and outlet of the tube, and (b) the hydraulic conductivity of the sand in the tube. Groundwater flows rapidly in the case of higher pressure (ΔH) or more permeable materials such as gravel or coarse sand, but flows slowly when the pressure difference is lower or the material is less permeable, such as fine sand or silt.
 
−
 
 
−
[[File:Newell-Article 1-Fig3..JPG|500px|thumbnail|right|Figure 3. Conceptual explanation of Darcy’s Law based on Darcy’s experiment (Adapted from course notes developed by Dr. R.J. Mitchell, Western Washington University).]]
 
−
Since&nbsp;Darcy’s&nbsp;time,&nbsp;Darcy’s Law has been extended to develop a useful variation of Darcy's formula that is used to to calculate the actual velocity that the groundwater is moving in units such as meters traveled per year. This quantity is called “interstitial velocity” or “seepage velocity” and is calculated by dividing the Darcy Velocity (flow per unit area) by the actual open pore area where groundwater is flowing, the “effective porosity”&nbsp;(Table 1):
 
−
 
 
−
[[File:Newell-Article 1-Equation 2r.jpg|400px]]
 
−
 
 
−
:Where:
 
−
::''V<sub>S</sub>'' = “interstitial velocity” or “seepage velocity” (units of length per time, such as m/sec)<br />
 
−
::''V<sub>D</sub>'' = “Darcy Velocity”; describes groundwater flow as the volume of flow per unit area per time (also units of length per time)<br />
 
−
::''n<sub>e</sub>'' = Effective porosity - fraction of cross section available for groundwater flow (unitless)
 
−
 
 
−
Effective porosity is smaller than total porosity. The difference is that total porosity includes some dead-end pores that do not support groundwater. Typical values for total and effective porosity are&nbsp;shown&nbsp;in&nbsp;Table&nbsp;1.
 
−
 
 
−
[[File:Newell-Article 1-Fig4.JPG|500px|thumbnail|left|Figure 4.  Difference between Darcy Velocity (also called Specific Discharge) and Seepage Velocity (also called Interstitial Velocity).]]
 
−
 
 
−
==Darcy Velocity and Seepage Velocity==
 
−
In&nbsp;groundwater&nbsp;calculations, Darcy Velocity and Seepage Velocity are used for different purposes. For any calculation where the actual flow rate in units of volume per time (such as liters per day or gallons per minute) is involved, then the original Darcy Equation should be used (calculate ''V<sub>D</sub>'', Equation 1) without using effective porosity. When calculating solute travel time however, the seepage velocity calculation (''V<sub>S</sub>'', Equation 2) must be used and an estimate of effective porosity is required. Figure 4 illustrates the differences between Darcy Velocity and&nbsp;Seepage&nbsp;Velocity.
 
  
−
==Mobile Porosity==
+
'''Contributors:''' Gorm Heron, Emily Crownover, Patrick Joyce, Ramona Iery
−
{| class="wikitable" style="float:right; margin-left:10px; text-align:center;"
 
−
|+Table 2.  Mobile porosity estimates from 15 tracer tests<ref name="Payne2008">Payne, F.C., Quinnan, J.A. and Potter, S.T., 2008. Remediation Hydraulics. CRC Press. ISBN 9780849372490  Available from: [https://www.routledge.com/Remediation-Hydraulics/Payne-Quinnan-Potter/p/book/9780849372490 CRC Press]</ref>
 
−
|-
 
−
!Aquifer Material
 
−
!Mobile Porosity<br /><small>(volume fraction)</small>
 
−
|-
 
−
|Poorly sorted sand and gravel||0.085
 
−
|-
 
−
|Poorly sorted sand and gravel||0.04-0.07
 
−
|-
 
−
|Poorly sorted sand and gravel||0.09
 
−
|-
 
−
|Fractured sandstone||0.001-0.007
 
−
|-
 
−
|Alluvial formation||0.102
 
−
|-
 
−
|Glacial outwash||0.145
 
−
|-
 
−
|Weathered mudstone regolith||0.07-0.10
 
−
|-
 
−
|Alluvial formation||0.07
 
−
|-
 
−
|Alluvial formation||0.07
 
−
|-
 
−
|Silty sand||0.05
 
−
|-
 
−
|Fractured sandstone||0.0008-0.001
 
−
|-
 
−
|Alluvium, sand and gravel||0.017
 
−
|-
 
−
|Alluvium, poorly sorted sand and gravel||0.003-0.017
 
−
|-
 
−
|Alluvium, sand and gravel||0.11-0.18
 
−
|-
 
−
|Siltstone, sandstone, mudstone||0.01-0.05
 
−
|}
 
  
−
Payne&nbsp;et&nbsp;al.&nbsp;(2008)&nbsp;reported the results from multiple short-term tracer tests conducted to aid the design of amendment injection systems<ref name="Payne2008" />. In these tests, the dissolved solutes were observed to migrate more rapidly through the aquifer than could be explained with typically reported values of ''n<sub>e</sub>''. They concluded that the heterogeneity of unconsolidated formations results in a relatively small area of an aquifer cross section carrying most of the water, and therefore solutes migrate more rapidly than expected. Based on these results, they recommend that a quantity called “mobile porosity” should be used in place of ''n<sub>e</sub>'' in equation 2 for calculating solute transport velocities. Based on 15 different tracer tests, typical values of mobile porosity range from 0.02 to 0.10 (Table 2). 
+
'''Key Resource:'''
 +
*Perfluoroalkyl and polyfluoroalkyl substances thermal desorption evaluation
  
−
A data mining analysis of 43 sites in California by Kulkarni et al. (2020) showed that on average 90% of the groundwater flow occurred in about 30% of cross sectional area perpendicular to groundwater flow. These data provided “moderate (but not confirmatory) support for the&nbsp;mobile&nbsp;porosity&nbsp;concept.”<ref name="Kulkarni2020">Kulkarni, P.R., Godwin, W.R., Long, J.A., Newell, R.C., Newell, C.J., 2020. How much heterogeneity? Flow versus area from a big data perspective. Remediation 30(2), pp. 15-23. [https://doi.org/10.1002/rem.21639 DOI: 10.1002/rem.21639] [//www.enviro.wiki/images/9/9b/Kulkarni2020.pdf Report.pdf]</ref>
+
==Introduction==
 +
Lysimeters are devices that are placed in the subsurface above the groundwater table to monitor the movement of water through the soil<ref name="GossEhlers2009">Goss, M.J., Ehlers, W., 2009. The Role of Lysimeters in the Development of Our Understanding of Soil Water and Nutrient Dynamics in Ecosystems. Soil Use and Management, 25(3), pp. 213–223. [https://doi.org/10.1111/j.1475-2743.2009.00230.x doi: 10.1111/j.1475-2743.2009.00230.x]</ref><ref>Pütz, T., Fank, J., Flury, M., 2018. Lysimeters in Vadose Zone Research. Vadose Zone Journal, 17 (1), pp. 1-4. [https://doi.org/10.2136/vzj2018.02.0035 doi: 10.2136/vzj2018.02.0035]&nbsp; [[Media: PutzEtAl2018.pdf | Open Access Article]]</ref><ref name="CostanzaEtAl2025">Costanza, J., Clabaugh, C.D., Leibli, C., Ferreira, J., Wilkin, R.T., 2025. Using Suction Lysimeters for Determining the Potential of Per- and Polyfluoroalkyl Substances to Leach from Soil to Groundwater: A Review. Environmental Science and Technology, 59(9), pp. 4215-4229. [https://doi.org/10.1021/acs.est.4c10246 doi: 10.1021/acs.est.4c10246]</ref>. Lysimeters have historically been used in agricultural sciences for monitoring nutrient or contaminant movement, soil moisture release curves, natural drainage patterns, and dynamics of plant-water interactions<ref name="GossEhlers2009"/><ref>Bergström, L., 1990. Use of Lysimeters to Estimate Leaching of Pesticides in Agricultural Soils. Environmental Pollution, 67 (4), 325–347. [https://doi.org/10.1016/0269-7491(90)90070-S doi: 10.1016/0269-7491(90)90070-S]</ref><ref>Dabrowska, D., Rykala, W., 2021. A Review of Lysimeter Experiments Carried Out on Municipal Landfill Waste. Toxics, 9(2), Article 26. [https://doi.org/10.3390/toxics9020026 doi: 10.3390/toxics9020026]&nbsp; [[Media: Dabrowska Rykala2021.pdf | Open Access Article]]</ref><ref>Fernando, S.U., Galagedara, L., Krishnapillai, M., Cuss, C.W., 2023. Lysimeter Sampling System for Optimal Determination of Trace Elements in Soil Solutions. Water, 15(18), Article 3277. [https://doi.org/10.3390/w15183277 doi: 10.3390/w15183277]&nbsp; [[Media: FernandoEtAl2023.pdf | Open Access Article]]</ref><ref name="MeissnerEtAl2020">Meissner, R., Rupp, H., Haselow, L., 2020. Use of Lysimeters for Monitoring Soil Water Balance Parameters and Nutrient Leaching. In: Climate Change and Soil Interactions. Elsevier, pp. 171-205. [https://doi.org/10.1016/B978-0-12-818032-7.00007-2 doi: 10.1016/B978-0-12-818032-7.00007-2]</ref><ref name="RogersMcConnell1993">Rogers, R.D., McConnell, J.W. Jr., 1993. Lysimeter Literature Review, Nuclear Regulatory Commission Report Numbers: NUREG/CR--6073, EGG--2706. [https://www.osti.gov/] ID: 10183270. [https://doi.org/10.2172/10183270 doi: 10.2172/10183270]&nbsp; [[Media: RogersMcConnell1993.pdf | Open  Access Article]]</ref><ref>Sołtysiak, M., Rakoczy, M., 2019. An Overview of the Experimental Research Use of Lysimeters. Environmental and Socio-Economic Studies, 7(2), pp. 49-56. [https://doi.org/10.2478/environ-2019-0012 doi: 10.2478/environ-2019-0012]&nbsp; [[Media: SołtysiakRakoczy2019.pdf | Open Access Article]]</ref><ref name="Stannard1992">Stannard, D.I., 1992. Tensiometers—Theory, Construction, and Use. Geotechnical Testing Journal, 15(1), pp. 48-58. [https://doi.org/10.1520/GTJ10224J doi: 10.1520/GTJ10224J]</ref><ref name="WintonWeber1996">Winton, K., Weber, J.B., 1996. A Review of Field Lysimeter Studies to Describe the Environmental Fate of Pesticides. Weed Technology, 10(1), pp. 202-209. [https://doi.org/10.1017/S0890037X00045929 doi: 10.1017/S0890037X00045929]</ref>. Recently, there has been strong interest in the use of lysimeters to measure and monitor movement of per- and polyfluoroalkyl substances (PFAS) through the vadose zone<ref name="Anderson2021">Anderson, R.H., 2021. The Case for Direct Measures of Soil-to-Groundwater Contaminant Mass Discharge at AFFF-Impacted Sites. Environmental Science and Technology, 55(10), pp. 6580-6583. [https://doi.org/10.1021/acs.est.1c01543 doi: 10.1021/acs.est.1c01543]</ref><ref name="AndersonEtAl2022">Anderson, R.H., Feild, J.B., Dieffenbach-Carle, H., Elsharnouby, O., Krebs, R.K., 2022. Assessment of PFAS in Collocated Soil and Porewater Samples at an AFFF-Impacted Source Zone: Field-Scale Validation of Suction Lysimeters. Chemosphere, 308(1), Article 136247. [https://doi.org/10.1016/j.chemosphere.2022.136247 doi: 10.1016/j.chemosphere.2022.136247]</ref><ref name="SchaeferEtAl2024">Schaefer, C.E., Nguyen, D., Fang, Y., Gonda, N., Zhang, C., Shea, S., Higgins, C.P., 2024. PFAS Porewater Concentrations in Unsaturated Soil: Field and Laboratory Comparisons Inform on PFAS Accumulation at Air-Water Interfaces. Journal of Contaminant Hydrology, 264, Article 104359. [https://doi.org/10.1016/j.jconhyd.2024.104359 doi: 10.1016/j.jconhyd.2024.104359]&nbsp; [[Media: SchaeferEtAl2024.pdf | Open Access Manuscript]]</ref><ref name="SchaeferEtAl2023">Schaefer, C.E., Lavorgna, G.M., Lippincott, D.R., Nguyen, D., Schaum, A., Higgins, C.P., Field, J., 2023. Leaching of Perfluoroalkyl Acids During Unsaturated Zone Flushing at a Field Site Impacted with Aqueous Film Forming Foam. Environmental Science and Technology, 57(5), pp. 1940-1948. [https://doi.org/10.1021/acs.est.2c06903 doi: 10.1021/acs.est.2c06903]</ref><ref name="SchaeferEtAl2022">Schaefer, C.E., Lavorgna, G.M., Lippincott, D.R., Nguyen, D., Christie, E., Shea, S., O’Hare, S., Lemes, M.C.S., Higgins, C.P., Field, J., 2022. A Field Study to Assess the Role of Air-Water Interfacial Sorption on PFAS Leaching in an AFFF Source Area. Journal of Contaminant Hydrology, 248, Article 104001. [https://doi.org/10.1016/j.jconhyd.2022.104001 doi: 10.1016/j.jconhyd.2022.104001]&nbsp; [[Media: SchaeferEtAl2022.pdf | Open Access Manuscript]]</ref><ref name="QuinnanEtAl2021">Quinnan, J., Rossi, M., Curry, P., Lupo, M., Miller, M., Korb, H., Orth, C., Hasbrouck, K., 2021. Application of PFAS-Mobile Lab to Support Adaptive Characterization and Flux-Based Conceptual Site Models at AFFF Releases. Remediation, 31(3), pp. 7-26. [https://doi.org/10.1002/rem.21680 doi: 10.1002/rem.21680]</ref>. PFAS are frequently introduced to the environment through land surface application and have been found to be strongly retained within the upper 5 feet of soil<ref name="BrusseauEtAl2020">Brusseau, M.L., Anderson, R.H., Guo, B., 2020. PFAS Concentrations in Soils: Background Levels versus Contaminated Sites. Science of The Total Environment, 740, Article 140017. [https://doi.org/10.1016/j.scitotenv.2020.140017 doi: 10.1016/j.scitotenv.2020.140017]</ref><ref name="BiglerEtAl2024">Bigler, M.C., Brusseau, M.L., Guo, B., Jones, S.L., Pritchard, J.C., Higgins, C.P., Hatton, J., 2024. High-Resolution Depth-Discrete Analysis of PFAS Distribution and Leaching for a Vadose-Zone Source at an AFFF-Impacted Site. Environmental Science and Technology, 58(22), pp. 9863-9874. [https://doi.org/10.1021/acs.est.4c01615 doi: 10.1021/acs.est.4c01615]</ref>. PFAS recalcitrance in the vadose zone means that environmental program managers and consultants need a cost-effective way of monitoring concentration conditions within the vadose zone. Repeated soil sampling and extraction processes are time consuming and only give a representative concentration of total PFAS in the matrix<ref name="NickersonEtAl2020">Nickerson, A., Maizel, A.C., Kulkarni, P.R., Adamson, D.T., Kornuc, J. J., Higgins, C.P., 2020. Enhanced Extraction of AFFF-Associated PFASs from Source Zone Soils. Environmental Science and Technology, 54(8), pp. 4952-4962. [https://doi.org/10.1021/acs.est.0c00792 doi: 10.1021/acs.est.0c00792]</ref>, not what is readily transportable in mobile porewater<ref name="SchaeferEtAl2023"/><ref name="StultsEtAl2024">Stults, J.F., Schaefer, C.E., Fang, Y., Devon, J., Nguyen, D., Real, I., Hao, S., Guelfo, J.L., 2024. Air-Water Interfacial Collapse and Rate-Limited Solid Desorption Control Perfluoroalkyl Acid Leaching from the Vadose Zone. Journal of Contaminant Hydrology, 265, Article 104382. [https://doi.org/10.1016/j.jconhyd.2024.104382 doi: 10.1016/j.jconhyd.2024.104382]&nbsp; [[Media: StultsEtAl2024.pdf | Open Access Manuscript]]</ref><ref name="StultsEtAl2023">Stults, J.F., Choi, Y.J., Rockwell, C., Schaefer, C.E., Nguyen, D.D., Knappe, D.R.U., Illangasekare, T.H., Higgins, C.P., 2023. Predicting Concentration- and Ionic-Strength-Dependent Air–Water Interfacial Partitioning Parameters of PFASs Using Quantitative Structure–Property Relationships (QSPRs). Environmental Science and Technology, 57(13), pp. 5203-5215. [https://doi.org/10.1021/acs.est.2c07316 doi: 10.1021/acs.est.2c07316]</ref><ref name="BrusseauGuo2022">Brusseau, M.L., Guo, B., 2022. PFAS Concentrations in Soil versus Soil Porewater: Mass Distributions and the Impact of Adsorption at Air-Water Interfaces. Chemosphere, 302, Article 134938. [https://doi.org/10.1016/j.chemosphere.2022.134938 doi: 10.1016/j.chemosphere.2022.134938]&nbsp; [[Media: BrusseauGuo2022.pdf | Open Access Manuscript]]</ref>. Fortunately, lysimeters have been found to be a viable option for monitoring the concentration of PFAS in the mobile porewater phase in the vadose zone<ref name="Anderson2021"/><ref name="AndersonEtAl2022"/>. Note that while some lysimeters, known as weighing lysimeters, can directly measure water flux, the most commonly utilized lysimeters in PFAS investigations only provide measurements of porewater concentrations.
  
−
==Advection-Dispersion-Reaction Equation==
+
==PFAS Background==
−
The transport of dissolved solutes in groundwater is often modeled using the Advection-Dispersion-Reaction (ADR) equation. As shown below (Equation 3), the ADR equation describes the change in dissolved solute concentration (''C'') over time (''t'') where groundwater flow is oriented along the ''x'' direction.
+
PFAS are a broad class of chemicals with highly variable chemical structures<ref>Moody, C.A., Field, J.A., 1999. Determination of Perfluorocarboxylates in Groundwater Impacted by Fire-Fighting Activity. Environmental Science and Technology, 33(16), pp. 2800-2806. [https://doi.org/10.1021/es981355+ doi: 10.1021/es981355+]</ref><ref name="MoodyField2000">Moody, C.A., Field, J.A., 2000. Perfluorinated Surfactants and the Environmental Implications of Their Use in Fire-Fighting Foams. Environmental Science and Technology, 34(18), pp. 3864-3870. [https://doi.org/10.1021/es991359u doi: 10.1021/es991359u]</ref><ref name="GlügeEtAl2020">Glüge, J., Scheringer, M., Cousins, I.T., DeWitt, J.C., Goldenman, G., Herzke, D., Lohmann, R., Ng, C.A., Trier, X., Wang, Z., 2020. An Overview of the Uses of Per- and Polyfluoroalkyl Substances (PFAS). Environmental Science: Processes and Impacts, 22(12), pp. 2345-2373. [https://doi.org/10.1039/D0EM00291G doi: 10.1039/D0EM00291G]&nbsp; [[Media: GlügeEtAl2020.pdf | Open Access Article]]</ref>. One characteristic feature of PFAS is that they are fluorosurfactants, distinct from more traditional hydrocarbon surfactants<ref name="MoodyField2000"/><ref name="Brusseau2018">Brusseau, M.L., 2018. Assessing the Potential Contributions of Additional Retention Processes to PFAS Retardation in the Subsurface. Science of The Total Environment, 613-614, pp. 176-185. [https://doi.org/10.1016/j.scitotenv.2017.09.065 doi: 10.1016/j.scitotenv.2017.09.065]&nbsp; [[Media: Brusseau2018.pdf | Open Access Manuscript]]</ref><ref>Dave, N., Joshi, T., 2017. A Concise Review on Surfactants and Its Significance. International Journal of Applied Chemistry, 13(3), pp. 663-672. [https://doi.org/10.37622/IJAC/13.3.2017.663-672 doi: 10.37622/IJAC/13.3.2017.663-672]&nbsp; [[Media: DaveJoshi2017.pdf  | Open Access Article]]</ref><ref>García, R.A., Chiaia-Hernández, A.C., Lara-Martin, P.A., Loos, M., Hollender, J., Oetjen, K., Higgins, C.P., Field, J.A., 2019. Suspect Screening of Hydrocarbon Surfactants in Afffs and Afff-Contaminated Groundwater by High-Resolution Mass Spectrometry. Environmental Science and Technology, 53(14), pp. 8068-8077. [https://doi.org/10.1021/acs.est.9b01895 doi: 10.1021/acs.est.9b01895]</ref>. Fluorosurfactants typically have a fully or partially fluorinated, hydrophobic tail with ionic (cationic, zwitterionic, or anionic) head group that is hydrophilic<ref name="MoodyField2000"/><ref name="GlügeEtAl2020"/>. The hydrophobic tail and ionic head group mean PFAS are very stable at hydrophobic adsorption interfaces when present in the aqueous phase<ref>Krafft, M.P., Riess, J.G., 2015. Per- and Polyfluorinated Substances (PFASs): Environmental Challenges. Current Opinion in Colloid and Interface Science, 20(3), pp. 192-212. [https://doi.org/10.1016/j.cocis.2015.07.004 doi: 10.1016/j.cocis.2015.07.004]</ref>. Examples of these interfaces include naturally occurring organic matter in soils and the air-water interface in the vadose zone<ref>Schaefer, C.E., Culina, V., Nguyen, D., Field, J., 2019. Uptake of Poly- and Perfluoroalkyl Substances at the Air–Water Interface. Environmental Science and Technology, 53(21), pp. 12442-12448. [https://doi.org/10.1021/acs.est.9b04008 doi: 10.1021/acs.est.9b04008]</ref><ref>Lyu, Y., Brusseau, M.L., Chen, W., Yan, N., Fu, X., Lin, X., 2018. Adsorption of PFOA at the Air–Water Interface during Transport in Unsaturated Porous Media. Environmental Science and Technology, 52(14), pp. 7745-7753. [https://doi.org/10.1021/acs.est.8b02348 doi: 10.1021/acs.est.8b02348]</ref><ref>Costanza, J., Arshadi, M., Abriola, L.M., Pennell, K.D., 2019. Accumulation of PFOA and PFOS at the Air-Water Interface. Environmental Science and Technology Letters, 6(8), pp. 487-491. [https://doi.org/10.1021/acs.estlett.9b00355 doi: 10.1021/acs.estlett.9b00355]</ref><ref>Li, F., Fang, X., Zhou, Z., Liao, X., Zou, J., Yuan, B., Sun, W., 2019. Adsorption of Perfluorinated Acids onto Soils: Kinetics, Isotherms, and Influences of Soil Properties. Science of The Total Environment, 649, pp. 504-514. [https://doi.org/10.1016/j.scitotenv.2018.08.209 doi: 10.1016/j.scitotenv.2018.08.209]</ref><ref>Nguyen, T.M.H., Bräunig, J., Thompson, K., Thompson, J., Kabiri, S., Navarro, D.A., Kookana, R.S., Grimison, C., Barnes, C.M., Higgins, C.P., McLaughlin, M.J., Mueller, J.F., 2020. Influences of Chemical Properties, Soil Properties, and Solution pH on Soil–Water Partitioning Coefficients of Per- and Polyfluoroalkyl Substances (PFASs). Environmental Science and Technology, 54(24), pp. 15883-15892. [https://doi.org/10.1021/acs.est.0c05705 doi: 10.1021/acs.est.0c05705]&nbsp; [[Media: NguyenEtAl2020.pdf  | Open Access Article]]</ref>. Their strong adsorption to both soil organic matter and the air-water interface is a major contributor to elevated concentrations of PFAS observed in the upper 5 feet of the soil column<ref name="BrusseauEtAl2020"/><ref name="BiglerEtAl2024"/>. While several other PFAS partitioning processes exist<ref name="Brusseau2018"/>, adsorption to solid phase soils and air-water interfaces are the two primary processes present at nearly all PFAS sites<ref>Brusseau, M.L., Yan, N., Van Glubt, S., Wang, Y., Chen, W., Lyu, Y., Dungan, B., Carroll, K.C., Holguin, F.O., 2019. Comprehensive Retention Model for PFAS Transport in Subsurface Systems. Water Research, 148, pp. 41-50. [https://doi.org/10.1016/j.watres.2018.10.035 doi: 10.1016/j.watres.2018.10.035]</ref>. The total PFAS mass obtained from a vadose zone soil sample contains the solid phase, air-water interfacial, and aqueous phase PFAS mass, which can be converted to porewater concentrations using Equation 1<ref name="BrusseauGuo2022"/>.</br>
 +
:: <big>'''Equation 1:'''</big>&nbsp;&nbsp; [[File: StultsEq1.png | 400 px]]</br>
 +
Where ''C<sub>p</sub>'' is the porewater concentration, ''C<sub>t</sub>'' is the total PFAS concentration, ''ρ<sub>b</sub>'' is the bulk density of the soil, ''θ<sub>w</sub>'' is the volumetric water content, ''R<sub>d</sub>'' is the PFAS retardation factor, ''K<sub>d</sub>'' is the solid phase adsorption coefficient, ''K<sub>ia</sub>'' is the air-water interfacial adsorption coefficient, and ''A<sub>aw</sub>'' is the air-water interfacial area. The air-water interfacial area of the soil is primarily a function of both the soil properties and the degree of volumetric water saturation in the soil. There are several methods of estimating air-water interfacial areas including thermodynamic functions based on the soil moisture retention curve. However, the thermodynamic function has been shown to underestimate air-water interfacial area<ref name="Brusseau2023">Brusseau, M.L., 2023. Determining Air-Water Interfacial Areas for the Retention and Transport of PFAS and Other Interfacially Active Solutes in Unsaturated Porous Media. Science of The Total Environment, 884, Article 163730. [https://doi.org/10.1016/j.scitotenv.2023.163730 doi: 10.1016/j.scitotenv.2023.163730]&nbsp; [[Media: Brusseau2023.pdf  | Open Access Article]]</ref>, and must typically be scaled using empirical scaling factors. An empirical method recently developed to estimate air-water interfacial area is presented in Equation 2<ref name="Brusseau2023"/>.</br>
 +
:: <big>'''Equation 2:'''</big>&nbsp;&nbsp; [[File: StultsEq2.png | 400 px]]</br>
 +
Where ''S<sub>w</sub>'' is the water phase saturation as a ratio of the water content over the volumetric soil porosity, and ''d<sub>50</sub>'' is the median grain diameter.
  
−
{|
+
==Lysimeters Background==
−
| || [[File:AdvectionEq3r.PNG|center|635px]]
+
[[File: StultsFig1.png | thumb | 600 px | Figure 1. (a) A field suction lysimeter with labeled parts typically used in field settings – Credit: Bibek Acharya and Dr. Vivek Sharma, UF/IFAS - https://edis.ifas.ufl.edu/publication/AE581. (b) Laboratory suction lysimeters used in Schaefer et al. 2024, which employed the use of micro-sampling suction lysimeters. (c) a field lysimeter used in Schaefer et al. 2023. (d) diagram of a drainage wicking lysimeter – Credit: Edaphic Scientific - https://edaphic.com.au/products/water/lysimeter-wick-for-drainage/]]
−
|-
+
Lysimeters, generally speaking, refer to instruments which collect water from unsaturated soils<ref name="MeissnerEtAl2020"/><ref name="RogersMcConnell1993"/>. However, there are multiple types of lysimeters which can be employed in field or laboratory settings. There are three primary types of lysimeters relevant to PFAS listed here and shown in Figure 1a-d.
−
| Where: ||
+
# <u>Suction Lysimeters (Figure 1a,b):</u> These lysimeters are the most relevant for PFAS sampling and are the majority of discussion in this article. These lysimeters operate by extracting liquid from the unsaturated vadose zone by applying negative suction pressure at the sampling head<ref name="CostanzaEtAl2025"/><ref name="SchaeferEtAl2024"/><ref name="QuinnanEtAl2021"/>. The sampling head is typically constructed of porous ceramic or stainless steel. A PVC case or stainless-steel case is attached to the sampling head and extends upward above the ground surface. Suction lysimeters are typically installed between 1 and 9 feet below ground surface, but can extend as deep as 40-60 feet in some cases<ref name="CostanzaEtAl2025"/>. Shallow lysimeters (< 10 feet) are typically installed using a hand auger. For ceramic lysimeters, a silica flour slurry should be placed at the base of the bore hole and allowed to cover the ceramic head before backfilling the hole partially with natural soil. Once the hole is partially backfilled with soil to cover the sampling head, the remainder of the casing should be sealed with hydrated bentonite chips. When sampling events occur, suction is applied at the ground surface using a rubber gasket seal and a hand pump or electric pump. After sufficient porewater is collected (the time for which can vary greatly based on the soil permeability and moisture content), the seal can be removed and a peristaltic pump used to extract liquid from the lysimeter.
−
|-
+
# <u>Field Lysimeters (Figure 1c):</u> These large lysimeters can be constructed from plastic or metal sidings. They can range from approximately 2 feet in diameter to as large as several meters in diameter<ref name="MeissnerEtAl2020"/>. Instrumentation such as soil moisture probes and tensiometers, or even multiple suction lysimeters, are typically placed throughout the lysimeter to measure the movement of water and determine characteristic soil moisture release curves<ref name="Stannard1992"/><ref name="WintonWeber1996"/><ref name="SchaeferEtAl2023"/><ref name="SchaeferEtAl2022"/><ref>van Genuchten, M.Th. , 1980. A Closed‐form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44(5), pp. 892-898. [https://doi.org/10.2136/sssaj1980.03615995004400050002x doi: 10.2136/sssaj1980.03615995004400050002x]</ref>. Water is typically collected at the base of the field lysimeter to determine net recharge through the system. These field lysimeters are intended to represent more realistic, intermediate scale conditions of field systems.
−
|
+
# <u>Drainage Lysimeters (Figure 1d):</u>  Also known as a “wick” lysimeter, these lysimeters typically consist of a hollow cup attached to a spout which protrudes above ground to relieve air pressure from the system and act as a sampling port. The hollow cup typically has filters and wicking devices at the base to collect water from the soil. The cup is filled with natural soil and collects water as it percolates through the vadose zone. These lysimeters are used to directly monitor net recharge from the vadose zone to the groundwater table and could be useful in determining PFAS mass flux.
−
:''D<sub>x</sub>, D<sub>y</sub>, and D<sub>z</sub>''&nbsp;&nbsp;
 
−
| are hydrodynamic dispersion coefficients in the ''x, y'' and ''z'' directions (L<sup>2</sup>/T),  
 
−
|-
 
−
|
 
−
:''v''
 
−
| is the advective transport or seepage velocity in the ''x'' direction (L/T), and
 
−
|-
 
−
|
 
−
:''R''
 
−
| is the linear, equilibrium retardation factor (see [[Sorption of Organic Contaminants]]),
 
−
|-
 
−
|
 
−
:''λ''
 
−
| is an effective first order decay rate due to combined biotic and abiotic processes (1/T).
 
−
|}
 
  
−
The term on the left side of the equation is the rate of mass change per unit volume. On the right side are terms representing the solute flux due to dispersion in the ''x, y'', and ''z'' directions, the advective flux in the ''x'' direction, and the first order decay due to biotic and abiotic processes. Dispersion coefficients (''D<sub>x,y,z</sub>'') are commonly estimated using the following relationships (Equation 4):
+
==Analysis of PFAS Concentrations in Soil and Porewater==
 +
[[File: StultsFig2.png | thumb | 500 px | Figure 2. Field Measured PFAS concentration Data (Orange) and Lab Core Measured Concentration Data (Blue) for four PFAS impacted sites<ref name="AndersonEtAl2022"/>]]
 +
Schaefer ''et al.''<ref name="SchaeferEtAl2024"/> measured PFAS porewater concentrations with field and laboratory suction lysimeters across several sites. Intact cores from the site were collected for soil water extraction using laboratory lysimeters. The lysimeters were used to directly compare field derived measurements of PFAS concentration in the mobile porewater phase. Results from measurements are for four sites presented in Figure 2.
  
−
{|
+
Data from sites A and B showed reasonably good agreement (within ½ order of magnitude) for most PFAS measured in the systems. At site C, more hydrophobic constituents (> C6 PFAS) tended to have higher concentrations in the lab core than the field site while less hydrophobic constituents (< C6) had higher concentrations in the field than lab cores. Site D showed substantially greater (1 order of magnitude or more) PFAS concentrations measured in the laboratory-collected porewater sample compared to what was measured in the field lysimeters. This discrepancy for the Site D soil can likely be attributed to soil heterogeneity (as indicated by ground penetrating radar) and the fact that the soil consisted of back-filled materials rather than undisturbed native soils.
−
| || [[File:AdvectionEq4.PNG|center|360px]]
+
−
|-
+
Site C showed elevated PFAS concentrations in the laboratory collected porewater for the more surface-active compounds. This increase was attributed to the soil wetting that occurred at the bench scale, which was reasonably described by the model shown in Equations 1 and 2 (see Table 1<ref name="AndersonEtAl2022"/>).
−
| Where: ||
 
−
|-
 
−
|
 
−
:''D<sub>m</sub>''
 
−
| is the molecular diffusion coefficient (L<sup>2</sup>/T), and  
 
−
|-
 
−
|
 
−
:''&alpha;<sub>L</sub>, &alpha;<sub>T</sub>'', and ''&alpha;<sub>V</sub>''&nbsp;&nbsp;
 
−
| are the longitudinal, transverse and vertical dispersivities (L), respectively.  
 
−
|}
 
  
−
===ADR Applications===
+
==Recommendations==
−
[[File:AdvectionFig5.png | thumb | right | 350px | Figure 5. Curves of concentration versus distance (a) and concentration versus time (b) generated by solving the ADR equation for a continuous source of a non-reactive tracer with ''R'' = 1, λ = 0, ''v'' = 5 m/yr, and ''D<sub>x</sub>'' = 10 m<sup>2</sup>/yr.]]
+
Recent research suggests:
−
The ADR equation can be solved to find the spatial and temporal distribution of solutes using a variety of analytical and numerical approaches.  The design tools [https://www.epa.gov/water-research/bioscreen-natural-attenuation-decision-support-system BIOSCREEN]<ref name="Newell1996">Newell, C.J., McLeod, R.K. and Gonzales, J.R., 1996. BIOSCREEN: Natural Attenuation Decision Support System - User's Manual, Version 1.3. US Environmental Protection Agency, EPA/600/R-96/087. [https://www.enviro.wiki/index.php?title=File:Newell-1996-Bioscreen_Natural_Attenuation_Decision_Support_System.pdf Report.pdf]  [https://www.epa.gov/water-research/bioscreen-natural-attenuation-decision-support-system BIOSCREEN website]</ref>, [https://www.epa.gov/water-research/biochlor-natural-attenuation-decision-support-system BIOCHLOR]<ref name="Aziz2000">Aziz, C.E., Newell, C.J., Gonzales, J.R., Haas, P.E., Clement, T.P. and Sun, Y., 2000. BIOCHLOR Natural Attenuation Decision Support System. User’s Manual - Version 1.0. US Environmental Protection Agency, EPA/600/R-00/008.  [https://www.enviro.wiki/index.php?title=File:Aziz-2000-BIOCHLOR-Natural_Attenuation_Dec_Support.pdf Report.pdf]  [https://www.epa.gov/water-research/biochlor-natural-attenuation-decision-support-system BIOCHLOR website]</ref>, and [https://www.epa.gov/water-research/remediation-evaluation-model-chlorinated-solvents-remchlor REMChlor]<ref name="Falta2007">Falta, R.W., Stacy, M.B., Ahsanuzzaman, A.N.M., Wang, M. and Earle, R.C., 2007. REMChlor Remediation Evaluation Model for Chlorinated Solvents - User’s Manual, Version 1.0. US Environmental Protection Agency. Center for Subsurface Modeling Support, Ada, OK.  [[Media:REMChlorUserManual.pdf | Report.pdf]]  [https://www.epa.gov/water-research/remediation-evaluation-model-chlorinated-solvents-remchlor REMChlor website]</ref> (see also [[REMChlor - MD]]) employ an analytical solution of the ADR equation.  [https://www.usgs.gov/software/mt3d-usgs-groundwater-solute-transport-simulator-modflow MT3DMS]<ref name="Zheng1999">Zheng, C. and Wang, P.P., 1999. MT3DMS: A Modular Three-Dimensional Multispecies Transport Model for Simulation of Advection, Dispersion, and Chemical Reactions of Contaminants in Groundwater Systems; Documentation and User’s Guide. Contract Report SERDP-99-1 U.S. Army Engineer Research and Development Center, Vicksburg, MS. [[Media:Mt3dmanual.pdf | Report.pdf]]  [https://www.usgs.gov/software/mt3d-usgs-groundwater-solute-transport-simulator-modflow MT3DMS website]</ref> uses a numerical method to solve the ADR equation using the head distribution generated by the groundwater flow model MODFLOW<ref name="McDonald1988">McDonald, M.G. and Harbaugh, A.W., 1988. A Modular Three-dimensional Finite-difference Ground-water Flow Model, Techniques of Water-Resources Investigations, Book 6, Modeling Techniques. U.S. Geological Survey, 586 pages. [https://doi.org/10.3133/twri06A1  DOI: 10.3133/twri06A1]  [[Media: McDonald1988.pdf | Report.pdf]]  Free MODFLOW download from: [https://www.usgs.gov/mission-areas/water-resources/science/modflow-and-related-programs?qt-science_center_objects=0#qt-science_center_objects USGS]</ref>.
+
*Successful thermal treatment of PFAS may require a higher target temperature than for other organics with similar boiling points
−
 
+
*Prevention of influx of water into treatment zone may be necessary.
−
Figures 5a and 5b were generated using a numerical solution of the ADR equation for a non-reactive tracer (''R'' = 1; λ = 0) with ''v'' = 5 m/yr and ''D<sub>x</sub>'' = 10 m<sup>2</sup>/yr.  Figure 5a shows the predicted change in concentration of the tracer, chloride, versus distance downgradient from the continuous contaminant source at different times (0, 1, 2, and 4 years).  Figure 5b shows the change in concentration versus time (commonly referred to as the breakthrough curve or BTC) at different downgradient distances (10, 20, 30 and 40 m).  At 2 years, the mid-point of the concentration versus distance curve (Figure 5a) is located 10 m downgradient (x = 5 m/yr * 2 yr).  At 20 m downgradient, the mid-point of the concentration versus time curves (Figure 5b) occurs at 4 years (t = 20 m / 5 m/yr).
+
Future studies should examine the potential for enhanced degradation during the thermal process by using soil amendments and/or manipulation of the local geochemistry to reduce the required treatment temperatures and therefore also reduce energy demand.
−
 
 
−
===Modeling Dispersion===
 
−
Mechanical&nbsp;dispersion (hydrodynamic dispersion) results from groundwater moving at rates both greater and less than the average linear velocity. This is due to: 1) fluids moving faster through the center of the pores than along the edges, 2) fluids traveling shorter pathways and/or splitting or branching to the sides, and 3) fluids traveling faster through larger pores than through smaller pores<ref>Fetter, C.W., 1994. Applied Hydrogeology: Macmillan College Publishing Company. New York New York. ISBN-13:978-0130882394</ref>. Because the invading solute-containing water does not travel at the same velocity everywhere, mixing occurs along flow paths. This mixing is called mechanical dispersion and results in distribution of the solute at the advancing edge of flow. The mixing that occurs in the direction of flow is called longitudinal dispersion. Spreading normal to the direction of flow from splitting and branching out to the sides is called transverse dispersion (Figure 6).  Typical values of the mechanical dispersivity measured in laboratory column tests are on the order of 0.01 to 1 cm<ref name="Anderson1979">Anderson, M.P. and Cherry, J.A., 1979. Using models to simulate the movement of contaminants through groundwater flow systems. Critical Reviews in Environmental Science and Technology, 9(2), pp.97-156.  [https://doi.org/10.1080/10643387909381669 DOI: 10.1080/10643387909381669]</ref>.
 
−
[[File:Fig2 dispanddiff.JPG|thumbnail|right|400px|Figure 6. Conceptual depiction of mechanical dispersion (adapted from ITRC (2011)<ref name="ITRC2011">ITRC Integrated DNAPL Site Strategy Team, 2011. Integrated DNAPL Site Strategy. Technical/Regulatory Guidance Document, 209 pgs. [//www.enviro.wiki/images/d/d9/ITRC-2011-Integrated_DNAPL.pdf Report pdf]</ref>).]]
 
−
 
 
−
The dispersion coefficient in the ADR equation accounts for the combined effects of mechanical dispersion and molecular diffusion, both of which cause spreading of the contaminant plume from highly concentrated areas toward less concentrated areas.  [[wikipedia:Molecular diffusion | Molecular diffusion]] is the result of the thermal motion of individual molecules which causes a flux of dissolved solutes from areas of higher concentration to areas of lower concentration.
 
−
 
 
−
===Modeling Diffusion===
 
−
[[File:Fig1 dispanddiff.JPG|thumbnail|left|400px|Figure 7. Conceptual depiction of diffusion of a dissolved chemical recently placed in a container at Time 1 (left panel) and then distributed throughout the container (right panel) at Time 2.]]
 
−
[[wikipedia: Molecular diffusion | Molecular&nbsp;diffusion]] is the result of the thermal motion of individual molecules which causes a flux of dissolved solutes from areas of higher concentration to areas of lower concentration (Figure 7). The diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the concentration gradient and is a function of the temperature and molecular weight. In locations where advective flux is low (clayey aquitards and sedimentary rock), diffusion is often the dominant transport mechanism.
 
−
 
 
−
The&nbsp;diffusive&nbsp;flux&nbsp;''J'' (M/L<sup>2</sup>/T) in groundwater is calculated using [[wikipedia:Fick's laws of diffusion | Fick’s Law]]:
 
−
 
 
−
{|
 
−
|
 
−
|<big>'''''J&nbsp;=&nbsp;-D<sub>e</sub>&nbsp;dC/dx'''''</big>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;(Equation&nbsp;5)
 
−
|-
 
−
|Where:||
 
−
|-
 
−
|
 
−
:''D<sub>e</sub>''
 
−
|is the effective diffusion coefficient and
 
−
|-
 
−
|
 
−
:''dC/dx''&nbsp;&nbsp;&nbsp;&nbsp;
 
−
|is the concentration gradient.
 
−
|}
 
−
The effective diffusion coefficient for transport through the porous media, ''D<sub>e</sub>, is estimated as:''
 
−
{|
 
−
|
 
−
|<big>'''''D<sub>e</sub>&nbsp;=&nbsp;D<sub>m</sub>&nbsp;n<sub>e</sub>&nbsp;&delta;/&Tau;'''''</big>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;(Equation&nbsp;6)
 
−
|-
 
−
|Where:||
 
−
|-
 
−
|
 
−
:''D<sub>m</sub>''&nbsp;&nbsp;&nbsp;&nbsp;
 
−
|is the [[wikipedia:Mass diffusivity | diffusion coefficient]] of the solute in water,
 
−
|-
 
−
|
 
−
:''n<sub>e</sub>''
 
−
|is the effective porosity (dimensionless),
 
−
|-
 
−
|
 
−
:''&delta;''
 
−
|is the constrictivity (dimensionless) which reflects the restricted motion of particles in narrow pores<ref name="Grathwohl1998">Grathwohl, P., 1998. Diffusion in Natural Porous Media: Contaminant Transport, Sorption/Desorption and Dissolution Kinetics. Kluwer Academic Publishers, Boston. DOI: 10.1007/978-1-4615-5683-1 Available from: [https://link.springer.com/book/10.1007/978-1-4615-5683-1 Springer.com]</ref>, and
 
−
|-
 
−
|
 
−
:''&Tau;''
 
−
|is the [[wikipedia:Tortuosity | tortuosity]] (dimensionless) which reflects the longer diffusion path in porous media around sediment particles<ref name="Carey2016">Carey, G.R., McBean, E.A. and Feenstra, S., 2016. Estimating Tortuosity Coefficients Based on Hydraulic Conductivity. Groundwater, 54(4), pp.476-487.  [https://doi.org/10.1111/gwat.12406 DOI:10.1111/gwat.12406] Available from: [https://ngwa.onlinelibrary.wiley.com/doi/abs/10.1111/gwat.12406 NGWA]</ref>.
 
−
|}
 
−
''D<sub>m</sub>'' is a function of the temperature, fluid viscosity and molecular weight.  Values of ''D<sub>m</sub>'' for common groundwater solutes are shown in Table 1.
 
−
 
 
−
{| class="wikitable" style="float:right; margin-left:20px; text-align:center;"
 
−
|+Table 1. Diffusion Coefficients (''D<sub>m</sub>'') for Common Groundwater Solutes.
 
−
|-
 
−
!Aqueous Diffusion Coefficient
 
−
!Temperature<br /><small>(&deg;C)</small>
 
−
!''D<sub>m</sub>''<br /><small>(cm<sup>2</sup>/s)</small>
 
−
!Reference
 
−
|-
 
−
|Acetone||25||&nbsp;&nbsp;1.16x10<sup>-5</sup>&nbsp;&nbsp;||Cussler 1997<ref name="Cussler1997">Cussler, E.L., 1997. Diffusion: Mass Transfer in Fluid Systems, Cambridge University Press, New York, 580 pages.  ISBN: 9780521450782</ref>
 
−
|-
 
−
|Benzene||20||1.02x10<sup>-5</sup>||Bonoli and Witherspoon 1968
 
−
|-
 
−
|Carbon dioxide||25||1.92x10<sup>-5</sup>||Cussler 1997<ref name="Cussler1997"/>
 
−
|-
 
−
|Carbon tetrachloride||25||9.55x10<sup>-6</sup>||Yaws 1995
 
−
|-
 
−
|Chloroform||25||1.08x10<sup>-5</sup>||Yaws 1995
 
−
|-
 
−
|Dichloroethene||25||1.12x10<sup>-5</sup>||Yaws 1995
 
−
|-
 
−
|1,4-Dioxane||25||1.02x10<sup>-5</sup>||Yaws 1995
 
−
|-
 
−
|Ethane||25||1.52x10<sup>-5</sup>||Witherspoon and Saraf 1965
 
−
|-
 
−
|Ethylbenzene||20||8.10x10<sup>-6</sup>||Bonoli and Witherspoon 1968
 
−
|-
 
−
|Ethene||25||1.87x10<sup>-5</sup>||Cussler 1997<ref name="Cussler1997"/>
 
−
|-
 
−
|Helium||25||6.28x10<sup>-5</sup>||Cussler 1997<ref name="Cussler1997"/>
 
−
|-
 
−
|Hydrogen||25||4.50x10<sup>-5</sup>||Cussler 1997<ref name="Cussler1997"/>
 
−
|-
 
−
|Methane||25||1.88x10<sup>-5</sup>||Witherspoon and Saraf 1965
 
−
|-
 
−
|Nitrogen||25||1.88x10<sup>-5</sup>||Cussler 1997<ref name="Cussler1997"/>
 
−
|-
 
−
|Oxygen||25||2.10x10<sup>-5</sup>||Cussler 1997<ref name="Cussler1997"/>
 
−
|-
 
−
|Perfluorooctanoic acid (PFOA)||20||4.80x10<sup>-6</sup>||Schaefer et al. 2019
 
−
|-
 
−
|Perfluorooctane sulfonic acid (PFOS)||20||5.40x10<sup>-6</sup>||Schaefer et al. 2019
 
−
|-
 
−
|Tetrachloroethene||25||8.99x10<sup>-6</sup>||Yaws 1995
 
−
|-
 
−
|Toluene||20||8.50x10<sup>-6</sup>||Bonoli and Witherspoon 1968
 
−
|-
 
−
|Trichloroethene||25||8.16x10<sup>-6</sup>||Rossi et al. 2015
 
−
|-
 
−
|Vinyl chloride||25||1.34x10<sup>-5</sup>||Yaws 1995
 
−
|}
 
−
 
 
−
<br clear="left" />
 
  
 
==References==
 
==References==
−
 
 
<references />
 
<references />
  
 
==See Also==
 
==See Also==
−
 
−
*[http://iwmi.dhigroup.com/solute_transport/advection.html International Water Management Institute Animations]
 
−
*[http://www2.nau.edu/~doetqp-p/courses/env303a/lec32/lec32.htm NAU Lecture Notes on Advective Transport]
 
−
*[https://www.youtube.com/watch?v=00btLB6u6DY MIT Open CourseWare Solute Transport: Advection with Dispersion Video]
 
−
*[https://www.youtube.com/watch?v=AtJyKiA1vcY Physical Groundwater Model Video]
 
−
*[https://www.coursera.org/learn/natural-attenuation-of-groundwater-contaminants/lecture/UzS8q/groundwater-flow-review Online Lecture Course - Groundwater Flow]
 

Latest revision as of 17:39, 9 January 2026

Lysimeters for Measuring PFAS Concentrations in the Vadose Zone

PFAS are frequently introduced to the environment through soil surface applications which then transport through the vadose zone to reach underlying groundwater receptors. Due to their unique properties and resulting transport and retention behaviors, PFAS in the vadose zone can be a persistent contaminant source to underlying groundwater systems. Determining the fraction of PFAS present in the mobile porewater relative to the total concentrations in soils is critical to understanding the risk posed by PFAS in vadose zone source areas. Lysimeters are instruments that have been used by agronomists and vadose zone researchers for decades to determine water flux and solute concentrations in unsaturated porewater. Lysimeters have recently been developed as a critical tool for field investigations and characterizations of PFAS impacted source zones.

Related Article(s):

Contributors: Gorm Heron, Emily Crownover, Patrick Joyce, Ramona Iery

Key Resource:

  • Perfluoroalkyl and polyfluoroalkyl substances thermal desorption evaluation

Introduction

Lysimeters are devices that are placed in the subsurface above the groundwater table to monitor the movement of water through the soil[1][2][3]. Lysimeters have historically been used in agricultural sciences for monitoring nutrient or contaminant movement, soil moisture release curves, natural drainage patterns, and dynamics of plant-water interactions[1][4][5][6][7][8][9][10][11]. Recently, there has been strong interest in the use of lysimeters to measure and monitor movement of per- and polyfluoroalkyl substances (PFAS) through the vadose zone[12][13][14][15][16][17]. PFAS are frequently introduced to the environment through land surface application and have been found to be strongly retained within the upper 5 feet of soil[18][19]. PFAS recalcitrance in the vadose zone means that environmental program managers and consultants need a cost-effective way of monitoring concentration conditions within the vadose zone. Repeated soil sampling and extraction processes are time consuming and only give a representative concentration of total PFAS in the matrix[20], not what is readily transportable in mobile porewater[15][21][22][23]. Fortunately, lysimeters have been found to be a viable option for monitoring the concentration of PFAS in the mobile porewater phase in the vadose zone[12][13]. Note that while some lysimeters, known as weighing lysimeters, can directly measure water flux, the most commonly utilized lysimeters in PFAS investigations only provide measurements of porewater concentrations.

PFAS Background

PFAS are a broad class of chemicals with highly variable chemical structures[24][25][26]. One characteristic feature of PFAS is that they are fluorosurfactants, distinct from more traditional hydrocarbon surfactants[25][27][28][29]. Fluorosurfactants typically have a fully or partially fluorinated, hydrophobic tail with ionic (cationic, zwitterionic, or anionic) head group that is hydrophilic[25][26]. The hydrophobic tail and ionic head group mean PFAS are very stable at hydrophobic adsorption interfaces when present in the aqueous phase[30]. Examples of these interfaces include naturally occurring organic matter in soils and the air-water interface in the vadose zone[31][32][33][34][35]. Their strong adsorption to both soil organic matter and the air-water interface is a major contributor to elevated concentrations of PFAS observed in the upper 5 feet of the soil column[18][19]. While several other PFAS partitioning processes exist[27], adsorption to solid phase soils and air-water interfaces are the two primary processes present at nearly all PFAS sites[36]. The total PFAS mass obtained from a vadose zone soil sample contains the solid phase, air-water interfacial, and aqueous phase PFAS mass, which can be converted to porewater concentrations using Equation 1[23].

Equation 1:   StultsEq1.png

Where Cp is the porewater concentration, Ct is the total PFAS concentration, ρb is the bulk density of the soil, θw is the volumetric water content, Rd is the PFAS retardation factor, Kd is the solid phase adsorption coefficient, Kia is the air-water interfacial adsorption coefficient, and Aaw is the air-water interfacial area. The air-water interfacial area of the soil is primarily a function of both the soil properties and the degree of volumetric water saturation in the soil. There are several methods of estimating air-water interfacial areas including thermodynamic functions based on the soil moisture retention curve. However, the thermodynamic function has been shown to underestimate air-water interfacial area[37], and must typically be scaled using empirical scaling factors. An empirical method recently developed to estimate air-water interfacial area is presented in Equation 2[37].

Equation 2:   StultsEq2.png

Where Sw is the water phase saturation as a ratio of the water content over the volumetric soil porosity, and d50 is the median grain diameter.

Lysimeters Background

Figure 1. (a) A field suction lysimeter with labeled parts typically used in field settings – Credit: Bibek Acharya and Dr. Vivek Sharma, UF/IFAS - https://edis.ifas.ufl.edu/publication/AE581. (b) Laboratory suction lysimeters used in Schaefer et al. 2024, which employed the use of micro-sampling suction lysimeters. (c) a field lysimeter used in Schaefer et al. 2023. (d) diagram of a drainage wicking lysimeter – Credit: Edaphic Scientific - https://edaphic.com.au/products/water/lysimeter-wick-for-drainage/

Lysimeters, generally speaking, refer to instruments which collect water from unsaturated soils[7][8]. However, there are multiple types of lysimeters which can be employed in field or laboratory settings. There are three primary types of lysimeters relevant to PFAS listed here and shown in Figure 1a-d.

  1. Suction Lysimeters (Figure 1a,b): These lysimeters are the most relevant for PFAS sampling and are the majority of discussion in this article. These lysimeters operate by extracting liquid from the unsaturated vadose zone by applying negative suction pressure at the sampling head[3][14][17]. The sampling head is typically constructed of porous ceramic or stainless steel. A PVC case or stainless-steel case is attached to the sampling head and extends upward above the ground surface. Suction lysimeters are typically installed between 1 and 9 feet below ground surface, but can extend as deep as 40-60 feet in some cases[3]. Shallow lysimeters (< 10 feet) are typically installed using a hand auger. For ceramic lysimeters, a silica flour slurry should be placed at the base of the bore hole and allowed to cover the ceramic head before backfilling the hole partially with natural soil. Once the hole is partially backfilled with soil to cover the sampling head, the remainder of the casing should be sealed with hydrated bentonite chips. When sampling events occur, suction is applied at the ground surface using a rubber gasket seal and a hand pump or electric pump. After sufficient porewater is collected (the time for which can vary greatly based on the soil permeability and moisture content), the seal can be removed and a peristaltic pump used to extract liquid from the lysimeter.
  2. Field Lysimeters (Figure 1c): These large lysimeters can be constructed from plastic or metal sidings. They can range from approximately 2 feet in diameter to as large as several meters in diameter[7]. Instrumentation such as soil moisture probes and tensiometers, or even multiple suction lysimeters, are typically placed throughout the lysimeter to measure the movement of water and determine characteristic soil moisture release curves[10][11][15][16][38]. Water is typically collected at the base of the field lysimeter to determine net recharge through the system. These field lysimeters are intended to represent more realistic, intermediate scale conditions of field systems.
  3. Drainage Lysimeters (Figure 1d): Also known as a “wick” lysimeter, these lysimeters typically consist of a hollow cup attached to a spout which protrudes above ground to relieve air pressure from the system and act as a sampling port. The hollow cup typically has filters and wicking devices at the base to collect water from the soil. The cup is filled with natural soil and collects water as it percolates through the vadose zone. These lysimeters are used to directly monitor net recharge from the vadose zone to the groundwater table and could be useful in determining PFAS mass flux.

Analysis of PFAS Concentrations in Soil and Porewater

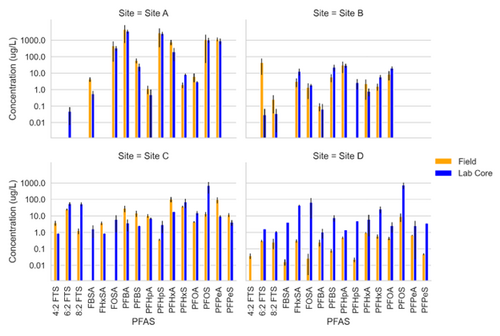
Figure 2. Field Measured PFAS concentration Data (Orange) and Lab Core Measured Concentration Data (Blue) for four PFAS impacted sites[13]

Schaefer et al.[14] measured PFAS porewater concentrations with field and laboratory suction lysimeters across several sites. Intact cores from the site were collected for soil water extraction using laboratory lysimeters. The lysimeters were used to directly compare field derived measurements of PFAS concentration in the mobile porewater phase. Results from measurements are for four sites presented in Figure 2.

Data from sites A and B showed reasonably good agreement (within ½ order of magnitude) for most PFAS measured in the systems. At site C, more hydrophobic constituents (> C6 PFAS) tended to have higher concentrations in the lab core than the field site while less hydrophobic constituents (< C6) had higher concentrations in the field than lab cores. Site D showed substantially greater (1 order of magnitude or more) PFAS concentrations measured in the laboratory-collected porewater sample compared to what was measured in the field lysimeters. This discrepancy for the Site D soil can likely be attributed to soil heterogeneity (as indicated by ground penetrating radar) and the fact that the soil consisted of back-filled materials rather than undisturbed native soils.

Site C showed elevated PFAS concentrations in the laboratory collected porewater for the more surface-active compounds. This increase was attributed to the soil wetting that occurred at the bench scale, which was reasonably described by the model shown in Equations 1 and 2 (see Table 1[13]).

Recommendations

Recent research suggests:

  • Successful thermal treatment of PFAS may require a higher target temperature than for other organics with similar boiling points
  • Prevention of influx of water into treatment zone may be necessary.

Future studies should examine the potential for enhanced degradation during the thermal process by using soil amendments and/or manipulation of the local geochemistry to reduce the required treatment temperatures and therefore also reduce energy demand.

References

  1. ^ 1.0 1.1 Goss, M.J., Ehlers, W., 2009. The Role of Lysimeters in the Development of Our Understanding of Soil Water and Nutrient Dynamics in Ecosystems. Soil Use and Management, 25(3), pp. 213–223. doi: 10.1111/j.1475-2743.2009.00230.x
  2. ^ Pütz, T., Fank, J., Flury, M., 2018. Lysimeters in Vadose Zone Research. Vadose Zone Journal, 17 (1), pp. 1-4. doi: 10.2136/vzj2018.02.0035  Open Access Article
  3. ^ 3.0 3.1 3.2 Costanza, J., Clabaugh, C.D., Leibli, C., Ferreira, J., Wilkin, R.T., 2025. Using Suction Lysimeters for Determining the Potential of Per- and Polyfluoroalkyl Substances to Leach from Soil to Groundwater: A Review. Environmental Science and Technology, 59(9), pp. 4215-4229. doi: 10.1021/acs.est.4c10246
  4. ^ Bergström, L., 1990. Use of Lysimeters to Estimate Leaching of Pesticides in Agricultural Soils. Environmental Pollution, 67 (4), 325–347. doi: 10.1016/0269-7491(90)90070-S
  5. ^ Dabrowska, D., Rykala, W., 2021. A Review of Lysimeter Experiments Carried Out on Municipal Landfill Waste. Toxics, 9(2), Article 26. doi: 10.3390/toxics9020026  Open Access Article
  6. ^ Fernando, S.U., Galagedara, L., Krishnapillai, M., Cuss, C.W., 2023. Lysimeter Sampling System for Optimal Determination of Trace Elements in Soil Solutions. Water, 15(18), Article 3277. doi: 10.3390/w15183277  Open Access Article
  7. ^ 7.0 7.1 7.2 Meissner, R., Rupp, H., Haselow, L., 2020. Use of Lysimeters for Monitoring Soil Water Balance Parameters and Nutrient Leaching. In: Climate Change and Soil Interactions. Elsevier, pp. 171-205. doi: 10.1016/B978-0-12-818032-7.00007-2
  8. ^ 8.0 8.1 Rogers, R.D., McConnell, J.W. Jr., 1993. Lysimeter Literature Review, Nuclear Regulatory Commission Report Numbers: NUREG/CR--6073, EGG--2706. [1] ID: 10183270. doi: 10.2172/10183270  Open Access Article
  9. ^ Sołtysiak, M., Rakoczy, M., 2019. An Overview of the Experimental Research Use of Lysimeters. Environmental and Socio-Economic Studies, 7(2), pp. 49-56. doi: 10.2478/environ-2019-0012  Open Access Article
  10. ^ 10.0 10.1 Stannard, D.I., 1992. Tensiometers—Theory, Construction, and Use. Geotechnical Testing Journal, 15(1), pp. 48-58. doi: 10.1520/GTJ10224J
  11. ^ 11.0 11.1 Winton, K., Weber, J.B., 1996. A Review of Field Lysimeter Studies to Describe the Environmental Fate of Pesticides. Weed Technology, 10(1), pp. 202-209. doi: 10.1017/S0890037X00045929
  12. ^ 12.0 12.1 Anderson, R.H., 2021. The Case for Direct Measures of Soil-to-Groundwater Contaminant Mass Discharge at AFFF-Impacted Sites. Environmental Science and Technology, 55(10), pp. 6580-6583. doi: 10.1021/acs.est.1c01543
  13. ^ 13.0 13.1 13.2 13.3 Anderson, R.H., Feild, J.B., Dieffenbach-Carle, H., Elsharnouby, O., Krebs, R.K., 2022. Assessment of PFAS in Collocated Soil and Porewater Samples at an AFFF-Impacted Source Zone: Field-Scale Validation of Suction Lysimeters. Chemosphere, 308(1), Article 136247. doi: 10.1016/j.chemosphere.2022.136247
  14. ^ 14.0 14.1 14.2 Schaefer, C.E., Nguyen, D., Fang, Y., Gonda, N., Zhang, C., Shea, S., Higgins, C.P., 2024. PFAS Porewater Concentrations in Unsaturated Soil: Field and Laboratory Comparisons Inform on PFAS Accumulation at Air-Water Interfaces. Journal of Contaminant Hydrology, 264, Article 104359. doi: 10.1016/j.jconhyd.2024.104359  Open Access Manuscript
  15. ^ 15.0 15.1 15.2 Schaefer, C.E., Lavorgna, G.M., Lippincott, D.R., Nguyen, D., Schaum, A., Higgins, C.P., Field, J., 2023. Leaching of Perfluoroalkyl Acids During Unsaturated Zone Flushing at a Field Site Impacted with Aqueous Film Forming Foam. Environmental Science and Technology, 57(5), pp. 1940-1948. doi: 10.1021/acs.est.2c06903
  16. ^ 16.0 16.1 Schaefer, C.E., Lavorgna, G.M., Lippincott, D.R., Nguyen, D., Christie, E., Shea, S., O’Hare, S., Lemes, M.C.S., Higgins, C.P., Field, J., 2022. A Field Study to Assess the Role of Air-Water Interfacial Sorption on PFAS Leaching in an AFFF Source Area. Journal of Contaminant Hydrology, 248, Article 104001. doi: 10.1016/j.jconhyd.2022.104001  Open Access Manuscript
  17. ^ 17.0 17.1 Quinnan, J., Rossi, M., Curry, P., Lupo, M., Miller, M., Korb, H., Orth, C., Hasbrouck, K., 2021. Application of PFAS-Mobile Lab to Support Adaptive Characterization and Flux-Based Conceptual Site Models at AFFF Releases. Remediation, 31(3), pp. 7-26. doi: 10.1002/rem.21680
  18. ^ 18.0 18.1 Brusseau, M.L., Anderson, R.H., Guo, B., 2020. PFAS Concentrations in Soils: Background Levels versus Contaminated Sites. Science of The Total Environment, 740, Article 140017. doi: 10.1016/j.scitotenv.2020.140017
  19. ^ 19.0 19.1 Bigler, M.C., Brusseau, M.L., Guo, B., Jones, S.L., Pritchard, J.C., Higgins, C.P., Hatton, J., 2024. High-Resolution Depth-Discrete Analysis of PFAS Distribution and Leaching for a Vadose-Zone Source at an AFFF-Impacted Site. Environmental Science and Technology, 58(22), pp. 9863-9874. doi: 10.1021/acs.est.4c01615
  20. ^ Nickerson, A., Maizel, A.C., Kulkarni, P.R., Adamson, D.T., Kornuc, J. J., Higgins, C.P., 2020. Enhanced Extraction of AFFF-Associated PFASs from Source Zone Soils. Environmental Science and Technology, 54(8), pp. 4952-4962. doi: 10.1021/acs.est.0c00792
  21. ^ Stults, J.F., Schaefer, C.E., Fang, Y., Devon, J., Nguyen, D., Real, I., Hao, S., Guelfo, J.L., 2024. Air-Water Interfacial Collapse and Rate-Limited Solid Desorption Control Perfluoroalkyl Acid Leaching from the Vadose Zone. Journal of Contaminant Hydrology, 265, Article 104382. doi: 10.1016/j.jconhyd.2024.104382  Open Access Manuscript
  22. ^ Stults, J.F., Choi, Y.J., Rockwell, C., Schaefer, C.E., Nguyen, D.D., Knappe, D.R.U., Illangasekare, T.H., Higgins, C.P., 2023. Predicting Concentration- and Ionic-Strength-Dependent Air–Water Interfacial Partitioning Parameters of PFASs Using Quantitative Structure–Property Relationships (QSPRs). Environmental Science and Technology, 57(13), pp. 5203-5215. doi: 10.1021/acs.est.2c07316
  23. ^ 23.0 23.1 Brusseau, M.L., Guo, B., 2022. PFAS Concentrations in Soil versus Soil Porewater: Mass Distributions and the Impact of Adsorption at Air-Water Interfaces. Chemosphere, 302, Article 134938. doi: 10.1016/j.chemosphere.2022.134938  Open Access Manuscript
  24. ^ Moody, C.A., Field, J.A., 1999. Determination of Perfluorocarboxylates in Groundwater Impacted by Fire-Fighting Activity. Environmental Science and Technology, 33(16), pp. 2800-2806. doi: 10.1021/es981355+
  25. ^ 25.0 25.1 25.2 Moody, C.A., Field, J.A., 2000. Perfluorinated Surfactants and the Environmental Implications of Their Use in Fire-Fighting Foams. Environmental Science and Technology, 34(18), pp. 3864-3870. doi: 10.1021/es991359u
  26. ^ 26.0 26.1 Glüge, J., Scheringer, M., Cousins, I.T., DeWitt, J.C., Goldenman, G., Herzke, D., Lohmann, R., Ng, C.A., Trier, X., Wang, Z., 2020. An Overview of the Uses of Per- and Polyfluoroalkyl Substances (PFAS). Environmental Science: Processes and Impacts, 22(12), pp. 2345-2373. doi: 10.1039/D0EM00291G  Open Access Article
  27. ^ 27.0 27.1 Brusseau, M.L., 2018. Assessing the Potential Contributions of Additional Retention Processes to PFAS Retardation in the Subsurface. Science of The Total Environment, 613-614, pp. 176-185. doi: 10.1016/j.scitotenv.2017.09.065  Open Access Manuscript
  28. ^ Dave, N., Joshi, T., 2017. A Concise Review on Surfactants and Its Significance. International Journal of Applied Chemistry, 13(3), pp. 663-672. doi: 10.37622/IJAC/13.3.2017.663-672  Open Access Article
  29. ^ García, R.A., Chiaia-Hernández, A.C., Lara-Martin, P.A., Loos, M., Hollender, J., Oetjen, K., Higgins, C.P., Field, J.A., 2019. Suspect Screening of Hydrocarbon Surfactants in Afffs and Afff-Contaminated Groundwater by High-Resolution Mass Spectrometry. Environmental Science and Technology, 53(14), pp. 8068-8077. doi: 10.1021/acs.est.9b01895
  30. ^ Krafft, M.P., Riess, J.G., 2015. Per- and Polyfluorinated Substances (PFASs): Environmental Challenges. Current Opinion in Colloid and Interface Science, 20(3), pp. 192-212. doi: 10.1016/j.cocis.2015.07.004
  31. ^ Schaefer, C.E., Culina, V., Nguyen, D., Field, J., 2019. Uptake of Poly- and Perfluoroalkyl Substances at the Air–Water Interface. Environmental Science and Technology, 53(21), pp. 12442-12448. doi: 10.1021/acs.est.9b04008
  32. ^ Lyu, Y., Brusseau, M.L., Chen, W., Yan, N., Fu, X., Lin, X., 2018. Adsorption of PFOA at the Air–Water Interface during Transport in Unsaturated Porous Media. Environmental Science and Technology, 52(14), pp. 7745-7753. doi: 10.1021/acs.est.8b02348
  33. ^ Costanza, J., Arshadi, M., Abriola, L.M., Pennell, K.D., 2019. Accumulation of PFOA and PFOS at the Air-Water Interface. Environmental Science and Technology Letters, 6(8), pp. 487-491. doi: 10.1021/acs.estlett.9b00355
  34. ^ Li, F., Fang, X., Zhou, Z., Liao, X., Zou, J., Yuan, B., Sun, W., 2019. Adsorption of Perfluorinated Acids onto Soils: Kinetics, Isotherms, and Influences of Soil Properties. Science of The Total Environment, 649, pp. 504-514. doi: 10.1016/j.scitotenv.2018.08.209
  35. ^ Nguyen, T.M.H., Bräunig, J., Thompson, K., Thompson, J., Kabiri, S., Navarro, D.A., Kookana, R.S., Grimison, C., Barnes, C.M., Higgins, C.P., McLaughlin, M.J., Mueller, J.F., 2020. Influences of Chemical Properties, Soil Properties, and Solution pH on Soil–Water Partitioning Coefficients of Per- and Polyfluoroalkyl Substances (PFASs). Environmental Science and Technology, 54(24), pp. 15883-15892. doi: 10.1021/acs.est.0c05705  Open Access Article
  36. ^ Brusseau, M.L., Yan, N., Van Glubt, S., Wang, Y., Chen, W., Lyu, Y., Dungan, B., Carroll, K.C., Holguin, F.O., 2019. Comprehensive Retention Model for PFAS Transport in Subsurface Systems. Water Research, 148, pp. 41-50. doi: 10.1016/j.watres.2018.10.035
  37. ^ 37.0 37.1 Brusseau, M.L., 2023. Determining Air-Water Interfacial Areas for the Retention and Transport of PFAS and Other Interfacially Active Solutes in Unsaturated Porous Media. Science of The Total Environment, 884, Article 163730. doi: 10.1016/j.scitotenv.2023.163730  Open Access Article
  38. ^ van Genuchten, M.Th. , 1980. A Closed‐form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Science Society of America Journal, 44(5), pp. 892-898. doi: 10.2136/sssaj1980.03615995004400050002x

See Also

Retrieved from "https://www.enviro.wiki/index.php?title=User:Jhurley/sandbox&oldid=17780"